ಪ್ರಯೋಗಗಳ ಡಿಸೈನ್ (ಡಿ.ಓ.ಇ.)

1920 ರ ದಶಕದಲ್ಲಿ ಸರ್ ರೊನಾಲ್ಡ್ ಫಿಶರ್ ಇವರು ಕೃಷಿ ಉತ್ಪಾದನೆಗಳಲ್ಲಿ ಸುಧಾರಣೆ ಮತ್ತು ಅಭಿವೃದ್ಧಿಯನ್ನು ಮಾಡಲು ತುಂಬಾ ಪ್ರಯತ್ನ ಪಟ್ಟಿದ್ದಾರೆ. ಫಿಶರ್ ಇವರನ್ನು ಸಂಖ್ಯಾಶಾಸ್ತ್ರದ ಶ್ರೇಷ್ಠ ಶಾಸ್ತ್ರಜ್ಞರಲ್ಲಿ ಒಬ್ಬರೆಂದು ವಿಶ್ವದಾದ್ಯಂತ ಪರಿಗಣಿಸಲಾಗುತ್ತಿತ್ತು. ಅಂದಿನ ಕಾಲದಲ್ಲಿ ಓಫ್ಯಾಟ್ (ವನ್-ಫ್ಯಾಕ್ಟರ್-ಎಟ್ ಎ ಟೈಮ್) ಎಂಬುದು ಖ್ಯಾತಿಯನ್ನು ಪಡೆದಿತ್ತು. ಅನೇಕ ಘಟಕಗಳಿಗೆ ಅವಲಂಬಿಸಿರುವ ಪ್ರಕ್ರಿಯೆಗಳ ಕುರಿತು ತಿಳಿದುಕೊಳ್ಳಲು ಒಂದು ಬಾರಿ ಒಂದೇ ಘಟಕದಲ್ಲಿ ಬದಲಾವಣೆಗಳನ್ನು ಮಾಡಿದಲ್ಲಿ ಅದರಿಂದ ಲಭಿಸುವ ಪರಿಣಾಮಗಳ ಕುರಿತಾದ ನಿರೀಕ್ಷಣೆಯನ್ನು ಮಾಡಲಾಗುತ್ತಿತ್ತು. ಈ ರೀತಿಯ ತಂತ್ರಜ್ಞಾನವನ್ನು ಓಫ್ಯಾಟ್ ಎಂಬುದಾಗಿ ಕರೆಯಲಾಗುತ್ತಿತ್ತು. ಫಿಶರ್ ಇವರು ಸಂಖ್ಯಾಶಾಸ್ತ್ರವನ್ನು ಉಪಯೋಗಿಸಿ ಅನೇಕ ವೆರಿಯೇಬಲ್ ಪ್ರಕ್ರಿಯೆಗಳ ಕುರಿತು ವಿಸ್ತಾರವಾದ ಮಾಹಿತಿ ಲಭ್ಯವಾಗಬಲ್ಲಂತಹ ಪ್ರಯೋಗಗಳ ವಿನ್ಯಾಸವನ್ನು (ಡಿಸೈನ್) ಯಶಸ್ವಿಯಾಗಿ ಮಾಡಿದರು. ಇದೇ ಈ ಪ್ರಕ್ರಿಯೆಯಲ್ಲಿರುವ ಮಹತ್ತರವಾದ ಕೊಡುಗೆಯಾಗಿದೆ.

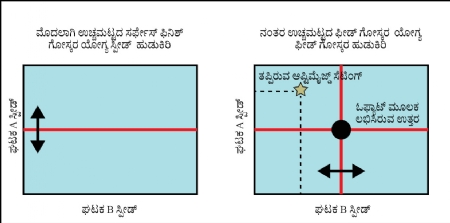
ಚಿತ್ರ ಕ್ರ. 1

ಪ್ರಯೋಗಗಳ ಕುರಿತು ಪಾರಂಪಾರಿಕ ದೃಷ್ಟಿಕೋನ

ವಿವಿಧ ಘಟಕಗಳ ಉತ್ಪಾದನೆಯಲ್ಲಿ ಮತ್ತು ಪ್ರಕ್ರಿಯೆಯಲ್ಲಿ ಯಾವ ಪರಿಣಾಮ ಉಂಟಾಗುತ್ತದೆ ಇದರ ಮೌಲ್ಯಮಾಪನವನ್ನು ಮಾಡುವುದಾದಲ್ಲಿ ಸಾಧಾರಣವಾಗಿ ನಾವು ಒಮ್ಮೆ ಒಂದೇ ಘಟಕಾಂಶದಲ್ಲಿ ಬದಲಾವಣೆಗಳನ್ನು ಮಾಡುತ್ತೇವೆ ಮತ್ತು ನಂತರ ಅದರ ಕುರಿತಾದ ನಿರೀಕ್ಷಣೆಯನ್ನು ನೊಂದಾಯಿಸುತ್ತೇವೆ. ಉದಾಹರಣೆ, ಕಟಿಂಗ್ ಸ್ಪೀಡ್ ಮತ್ತು ಫೀಡ್ ಈ ಎರಡೂ ಘಟಕಗಳ ಸೆಟಿಂಗ್ ಆಪ್ಟಿಮೈಜ್ಡ್ ಮಾಡುವುದಾದಲ್ಲಿ, ಓಫ್ಯಾಟ್ ನ ಪಾರಂಪಾರಿಕ ರೀತಿಗೆ ಅನುಸಾರವಾಗಿ ನಾವು ಮೊದಲು ಉಚ್ಚಮಟ್ಟದ ಸರ್ಫೇಸ್ ಫಿನಿಶ್ ಪಡೆಯಲು ಯಾವ ಕಟಿಂಗ್ ಸ್ಪೀಡ್ ಹೆಚ್ಚು ಸೂಕ್ತವಾಗಿದೆ, ಎಂಬುದನ್ನು ಹುಡುಕಬಲ್ಲೆವು. ಇದರ ನಂತರ ಆ ಕಟಿಂಗ್ ಸ್ಪೀಡ್ ನಲ್ಲಿ ಯಾವ ರೀತಿಯ ಫೀಡ್ ಉಟ್ಟಮಟ್ಟದ ಸರ್ಫೇಸ್ ಫಿನಿಶ್ ನೀಡಬಲ್ಲದು, ಎಂಬುದನ್ನು ಹುಡುಕೋಣ. ಆದರೂ ಕೂಡಾ ಓಫ್ಯಾಟ್ ನಲ್ಲಿರುವ ವಿವಿಧ ಘಟಕಗಳಲ್ಲಾಗುವ ಪರಸ್ಪರ ಇಂಟರ್ಯಾಕ್ಷನ್ ತಿಳಿಯಲಾರದು. ಇಂಟರೇಕ್ಷನ್ ಅಂದರೆ ಒಂದು ಘಟಕದಲ್ಲಾಗುವ ಬದಲಾವಣೆಗಳಿಂದ ಇನ್ನಿತರ ಘಟಕಗಳ ಸೆಟಿಂಗ್ ನಲ್ಲಿ ಬೀರುವ ಪ್ರಭಾವ. ಓಫ್ಯಾಟ್ ನಲ್ಲಿ ಈ ಇಂಟರೇಕ್ಷನ್ ಗಳ ಕುರಿತು ಯಾವುದೇ ರೀತಿಯಲ್ಲಿ ವಿಚಾರ ಮಾಡದಿರುವುದರಿಂದ ಅದರಿಂದ ಲಭಿಸುವ ಸ್ಪೀಡ್ ಮತ್ತು ಫೀಡ್ ಇವುಗಳ ಉಚ್ಚಮಟ್ಟದ ಸೆಟಿಂಗ್ ಮಾತ್ರ ನಿಜವಾಗಿಯೂ ಆಪ್ಟಿಮೈಜ್ಡ್ ಇರಬಲ್ಲದು, ಎಂದು ಹೇಳಲಾಗುವುದಿಲ್ಲ. (ಚಿತ್ರ ಕ್ರ. 1 ನೋಡಿರಿ).

ಇದರಿಂದಾಗಿ ತಜ್ಞರಿಂದ ಸಂಖ್ಯಾಶಾಸ್ತ್ರವನ್ನು ಬಳಸಿ ಡಿಸೈನ್ ಮಾಡಿರುವ ಪ್ರಯೋಗಗಳ ಸ್ಟ್ಯಾಟಿಸ್ಟಿಕಲಿ ಡಿಸೈನ್ಡ್ ಎಕ್ಸ್ಪರಿಮೆಂಟ್ (ಎಸ್.ಡಿ.ಇ.) ಸೂಚಿಸಲಾಗುತ್ತದೆ. ಡಿ.ಓ.ಇ. (ಡಿಸೈನ್ ಆಫ್ ಎಕ್ಸ್ಪರಿಮೆಂಟ್ಸ್) ಇದು ಇದರ ಪ್ರಸಿದ್ಧ ಹೆಸರಾಗಿದೆ. ಕಡಿಮೆ ಪ್ರಮಾಣದ ಪರೀಕ್ಷೆಗಳಲ್ಲಿ ಹೆಚ್ಚು ವಿಷಯಗಳನ್ನು ಅರಿತುಕೊಳ್ಳುವುದು ಸಾಧ್ಯ, ಇದೇ ಡಿ.ಓ.ಇ.ಯಿಂದ ಲಭಿಸುವ ಮಹತ್ವದ ಲಾಭವಾಗಿದೆ.

ಇದರಲ್ಲಿ ಪ್ರಯೋಗಗಳನ್ನು LF ಎಂಬುದಾಗಿ ಕರೆಯಲಾಗುತ್ತದೆ. ಇದರಲ್ಲಿ F ಇದು ಘಟಕಗಳ ಸಂಖ್ಯೆಯಾಗಿದೆ ಮತ್ತು L ಇದು ಘಟಕಗಳಲ್ಲಿರುವ ಹಂತಗಳ ಸಂಖ್ಯೆಯಾಗಿದೆ. ಉದಾಹರಣೆ, ಒಂದು ವೇಳೆ ಯಾವುದೇ ಪ್ರಕ್ರಿಯೆಯ ಮೂರು ಘಟಕಗಳಿದ್ದಲ್ಲಿ ಮತ್ತು ಪ್ರತಿಯೊಂದು ಘಟಕಗಳಲ್ಲಿ ಎರಡು ಹಂತಗಳಿವೆ. ಆದರೆ ಇದಕ್ಕೋಸ್ಕರ 23 ಅಂದರೆ 8 ಪ್ರಯೋಗಗಳನ್ನು ಮಾಡಬೇಕಾಗುತ್ತದೆ. ಇದನ್ನೇ ಒಂದು ಪುನರಾವರ್ತನೆಯಾಗುವ ಪ್ರಯೋಗ (ರೆಪ್ಲಿಕೇಟ್) ಎಂದು ಹೇಳುತ್ತಾರೆ.

ಅದರಂತೆಯೇ ಒಂದು ವೇಳೆ ಪ್ರತಿ 3 ಸ್ತರಗಳಲ್ಲಿರುವ 5 ಘಟಕಗಳಿದ್ದರೂ ಕೂಡಾ ಅದು 35 ಪ್ರಯೋಗವಾಗಬಲ್ಲದು. ಅದರ 3*3*3*3*3 ಅಂದರೆ 243 ಪರೀಕ್ಷೆಗಳಿರಬಲ್ಲವು. ಘಟಕ ಮತ್ತು ಸ್ತರಗಳ

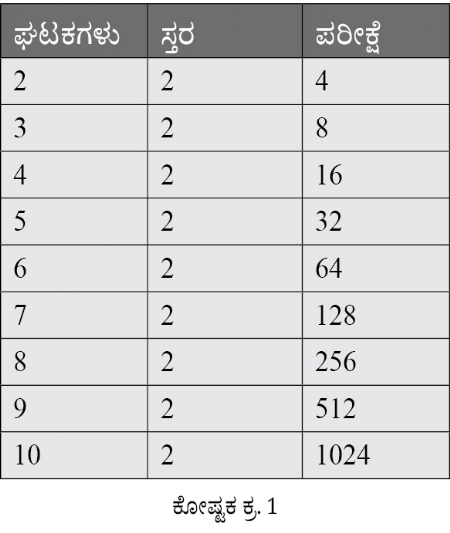
ಸಂಖ್ಯೆಯು ಹೆಚ್ಚಾದಂತೆ ಪರೀಕ್ಷೆಗಳ ಸಂಖ್ಯೆಯೂ ವೃದ್ಧಿಸಬಲ್ಲದು, ಎಂಬ ಅಂಶವು ಇದರಿಂದ ಗಮನಕ್ಕೆ ಬರುತ್ತದೆ. (ಕೋಷ್ಟಕ ಕ್ರ. 1 ನೋಡಿರಿ).

ಪರೀಕ್ಷೆಗಳ ಸಂಖ್ಯೆಯ ಪ್ರಮಾಣ ಹೆಚ್ಚಾಗಬಾರದು ಎಂಬುದಕ್ಕಾಗಿಯೇ ಹೆಚ್ಚಿನ ಪ್ರಯೋಗಗಳಲ್ಲಿ ಪ್ರತಿಯೊಂದು ಘಟಕಗಳ ಎರಡು ಸ್ತರಗಳ ಕುರಿತು ವಿಚಾರ ಮಾಡಲಾಗುತ್ತದೆ. ಒಂದು ವೇಳೆ ಘಟಕಗಳ ಸಂಖ್ಯೆಯು ‘K’ ಇದ್ದಲ್ಲಿ ಮತ್ತು ಪ್ರತಿಯೊಂದರ ಎರಡು ಸ್ತರಗಳಿದ್ದಲ್ಲಿ, ಪ್ರಯೋಗಕ್ಕೋಸ್ಕರ 2K ಇಷ್ಟು ಪರೀಕ್ಷೆಗಳನ್ನು ಮಾಡಬೇಕಾಗುತ್ತದೆ. ಈ ಪ್ರಯೋಗಗಳ ಒಂದು ಚಿತ್ರವು ಇರಬಲ್ಲದು. ಈ ಪ್ರಯೋಗಗಳಲ್ಲಿ ನಿಖರತೆಯನ್ನು ಹೆಚ್ಚಿಸಲು ಸಂಪೂರ್ಣ ಪ್ರಯೋಗವನ್ನು ಪುನಃ ಮಾಡುವ ಆವಶ್ಯಕತೆ ಇರುತ್ತದೆ.

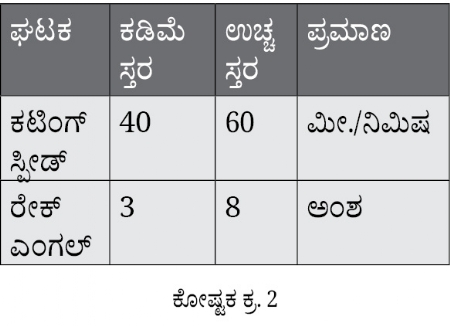
ಪ್ರಯೋಗಗಳ ಡಿಸೈನ್ ಈ ಕಲ್ಪನೆಯ ಮೂಲಭೂತ ಅಂಶಗಳನ್ನು ತಿಳಿದುಕೊಳ್ಳಲು ಒಂದು ಯಂತ್ರಣೆಯ ಪ್ರಕ್ರಿಯೆಯಲ್ಲಿ ಟೂಲ್ ನ ಬಾಳಿಕೆಯನ್ನು ವೃದ್ಧಿಸಲು ಕಟಿಂಗ್ ನ ಆಪ್ಟಿಮೈಜ್ಡ್ ಪ್ಯಾರಾಮೀಟರ್ ಹುಡುಕುವ ಪ್ರಯೋಗದ ಕುರಿತು ವಿಚಾರ ಮಾಡೋಣ. ಯಂತ್ರಣೆಯ ಪ್ರಕ್ರಿಯೆಯಲ್ಲಿ ಟೂಲ್ ನ ಬಾಳಿಕೆಯಲ್ಲಿ ಪ್ರಭಾವವನ್ನು ಬೀರುವ ಕಟಿಂಗ್ ಸ್ಪೀಡ್ (ಮೀಟರ್/ ನಿಮಿಷ) ಮತ್ತು ರೇಕ್ ಎಂಗಲ್ ಇಂತಹ ಎರಡು ಘಟಕಗಳ ಕುರಿತು ವಿಚಾರ ಮಾಡೋಣ. ಲೋಹಗಳನ್ನು ಕತ್ತರಿಸುವ ಮೂಲಭೂತ ತಂತ್ರ ಮತ್ತು ತಮಗಿರುವ ಅನುಭವದ ಸಹಾಯದಿಂದ ಈ ಪ್ರಯೋಗದಲ್ಲಿ ಈ ಎರಡು ಘಟಕಗಳು ಯಾವ ಹಂತದಲ್ಲಿ ಬಳಸಬೇಕು, ಎಂಬುದನ್ನು ನಿರ್ಧರಿಸಬಹುದು. ಈ ಕುರಿತು ತಮಗಿರುವ ತಿಳುವಳಿಕೆಗೆ ಅನುಸಾರವಾಗಿ ಯಾವ ಘಟಕ ಅಥವಾ ಅದರ ಯಾವ ಮೌಲ್ಯವು ಸೂಕ್ತವಲ್ಲವೋ, ಅದಕ್ಕೋಸ್ಕರ ಸಮಯವನ್ನು ವ್ಯರ್ಥಗೊಳಿಸುವಲ್ಲಿ ಯಾವುದೇ ಅರ್ಥವಿಲ್ಲ. ಇದರಿಂದಾಗಿ ತಮಗಿರುವ ಅನುಭವದಿಂದಲೇ ಪ್ರತಿಯೊಂದು ಘಟಕಗಳ ಎರಡು ಸ್ತರಗಳನ್ನು ಪ್ರಯೋಗಕ್ಕೋಸ್ಕರ ಬಳಸಲಾಗುತ್ತದೆ. ಪ್ಯಾರಾಮೀಟರ್ ಗಳ ಈ ಹಂತದಲ್ಲಿ ಸಂಶೋಧನೆಯನ್ನು ಮಾಡಿ ಅದರಿಂದ ಲಭಿಸುವ ಆಯಾಮಗಳನ್ನು (ಇಲ್ಲಿ ಟೂಲ್ ಗಳ ಬಾಳಿಕೆ) ಆಪ್ಟಿಮೈಜ್ ಮಾಡುವಲ್ಲಿ ನಾವು ಪ್ರಯತ್ನಿಸಲಿದ್ದೇವೆ. ಕೋಷ್ಟಕ ಕ್ರ. 2 ರಲ್ಲಿ ನೀಡಿರುವ ಘಟಕಗಳ ಉಚ್ಚಮಟ್ಟ ಮತ್ತು ಕಡಿಮೆ ಹಂತಗಳನ್ನು ನಾವು ನಿರ್ಧರಿಸಿರುತ್ತೇವೆ. ಇವುಗಳಿಗೆ ಒಮ್ಮೊಮ್ಮೆ ಘಟಕಗಳ ಗುಣಧರ್ಮ ಎಂಬುದಾಗಿಯೂ ಕರೆಯಲಾಗುತ್ತದೆ.

ಈಗ ನಾವು ಈ ಘಟಕಗಳು ಮತ್ತು ಸ್ತರಗಳಿಗೆ ಒಂದು ಮ್ಯಾಟ್ರಿಕ್ಸ್ ರಚನೆಯನ್ನು ತಯಾರಿಸೋಣ. ಈ ರಚನೆಯನ್ನು ‘ಫುಲ್ ಫ್ಯಾಕ್ಟೋರಿಯಲ್ ಡಿಸೈನ್’ (ಎಫ್.ಎಫ್.ಡಿ.) ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಎಫ್.ಎಫ್.ಡಿ.ಯಲ್ಲಿ ಪ್ರತಿಯೊಂದು ಘಟಕಗಳ ಪ್ರತಿಯೊಂದು ಸ್ತರದ ಪರೀಕ್ಷೆಯನ್ನು ಮಾಡಲಾಗುತ್ತದೆ. ಅಂದರೆ, ಈ ಪ್ರಯೋಗದಲ್ಲಿ 2*2=4 ಪರೀಕ್ಷೆಯನ್ನು ಮಾಡಲಾಗುತ್ತದೆ.

ಈ ಹಿಂದೆ ಉಲ್ಲೇಖಿಸಿದಂತೆ ಎಫ್.ಎಫ್.ಡಿ. ಯಲ್ಲಿರುವ ಪರೀಕ್ಷೆಗಳ ಸಂಖ್ಯೆ N = (ಸ್ತರ ಘಟಕ) ಎಂಬುದಾಗಿರುತ್ತದೆ. ಪ್ರತಿಯೊಂದು ಘಟಕ ಪ್ರತಿಯೊಂದು ಇನ್ನಿತರ ಘಟಕಗಳ ಪ್ರತಿಯೊಂದು ಸ್ತರದಲ್ಲಿ ಪರೀಕ್ಷಿಸಬೇಕು, ಆದ್ದರಿಂದ ಕೋಷ್ಟಕ ಕ್ರ. 3 ಕ್ಕೆ ಅನುಸಾರವಾಗಿ ಪ್ರಯೋಗವನ್ನು ಮಾಡಲಾಗುತ್ತದೆ. ಈ ಕೋಷ್ಟಕದಲ್ಲಿ ಪ್ರಯೋಗದಿಂದ ಲಭಿಸಿರುವ ಟೂಲ್ ಗಳ ಬಾಳಿಕೆಯ ಕುರಿತಾದ ಮಾಹಿತಿಯನ್ನು ವಿಶ್ಲೇಷಣೆಗೋಸ್ಕರ ನೀಡಲಾಗಿದೆ. ಈ ಎಲ್ಲ ಪರೀಕ್ಷೆಗಳನ್ನು ರೆಂಡಮ್ ಆರ್ಡರ್ ನಲ್ಲಿ ಮಾಡಬೇಕು. ಆದ್ದರಿಂದ ಈ ಪ್ರಯೋಗದಲ್ಲಿ ಇಲ್ಲದಿರುವ ಇನ್ನಿತರ ಘಟಕಗಳ ಅಂತಿಮ ಉತ್ತರಕ್ಕೋಸ್ಕರ ಯಾವುದೇ ರೀತಿಯ ಗಂಭೀರ ಪರಿಣಾಮ ಬೀರಲ್ಪಡುವುದಿಲ್ಲ, ಎಂಬುದರ ಕುರಿತಾದ ಮುಂಜಾಗ್ರತೆಯನ್ನು ವಹಿಸುವ ಸಲಹೆಯನ್ನು ಸಂಖ್ಯಾಶಾಸ್ತ್ರಜ್ಞರು ಕೊಡುತ್ತಾರೆ.

ಈಗ ಈ ಪ್ರಯೋಗದಿಂದ ಲಭಿಸಿರುವ ಆಯಾಮಗಳ ವಿಶ್ಲೇಷಣೆಯನ್ನು ಹೇಗೆ ಮಾಡಬೇಕು ಎಂಬುದರ ಕುರಿತು ತಿಳಿದುಕೊಳ್ಳೋಣ. ಪ್ರತಿಯೊಂದು ಘಟಕಗಳ ಪ್ರಭಾವವನ್ನು ಪರಿಶೀಲಿಸಲು ಮಹತ್ವಪೂರ್ಣವಾದ ಸೂತ್ರಗಳು ಈ ಮುಂದಿನಂತಿವೆ.

ಈ ಸೂತ್ರಗಳೆಂದರೆ ಪ್ರತಿಯೊಂದು ಘಟಕಗಳ ಪ್ರಮುಖ ಪ್ರಭಾವಗಳಿಗೋಸ್ಕರ ಹಾಗೆಯೇ ಘಟಕಗಳಲ್ಲಿರುವ ಇಂಟರೇಕ್ಷನ್ ಗಳಿಗೂ ಅನ್ವಯಿಸುತ್ತದೆ. ಮೊದಲಾಗಿ ನಾವು ರೇಕ್ ಎಂಗಲ್ ಎಂಬ ಘಟಕದ ಪ್ರಮುಖ ಪ್ರಭಾವದ

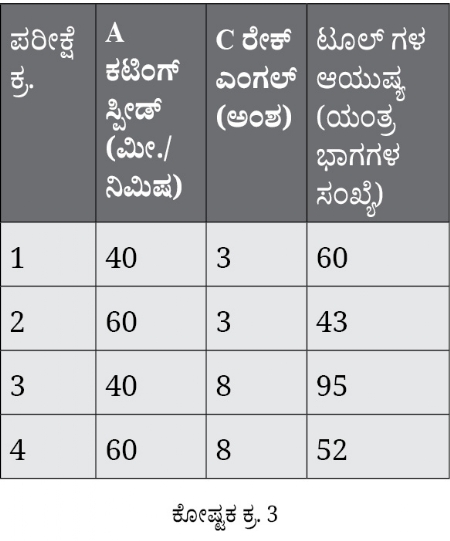
ಅಳತೆಯನ್ನು ಮಾಡೋಣ. ಕೋಷ್ಟಕ ಕ್ರ. 3 ಕ್ಕೆ ಅನುಸಾರವಾಗಿ ಇದರ ಗಣನೆಯನ್ನು ಮಾಡುವುದು ಎಲ್ಲಕ್ಕಿಂತಲೂ ಸುಲಭವಾಗಿದೆ, ಎಂಬ ಅಂಶವು ಗಮನಕ್ಕೆ ಬರುತ್ತದೆ.

ರೇಕ್ ಎಂಗಲ್ ನ ಉಚ್ಚಮಟ್ಟದಲ್ಲಿರುವ (8°) ಸರಾಸರಿ ಮೌಲ್ಯ (95+52)/2=73.5.

ಇದೇ ರೀತಿಯಲ್ಲಿ ರೇಕ್ ಎಂಗಲ್ ನ ಅರ್ಧ ಸ್ತರದಲ್ಲಿ (3°) ಸರಾಸರಿ ಮೌಲ್ಯವು (60+43)/2=51.5

ಇದರಿಂದಾಗಿ ಟೂಲ್ ನ ಬಾಳಿಕೆಯಲ್ಲಿ ರೇಕ್ ಎಂಗಲ್ ಪ್ರಭಾವ (73.5-51.5)=22 ರಷ್ಟು ಇದೆ. ಇದು ಧನಾತ್ಮಕ (ಪಾಸಿಟಿವ್) ಸಂಖ್ಯೆಯಾಗಿದೆ. ರೇಕ್ ಎಂಗಲ್ 3° ಯಿಂದ 8° ತನಕ ಹೆಚ್ಚಾಗಬಲ್ಲದು, ಹಾಗೆಯೇ ಟೂಲ್ ನ ಬಾಳಿಕೆ ಸರಾಸರಿ 22 ಯಂತ್ರಭಾಗಗಳಷ್ಟು ಸುಧಾರಿಸಬಲ್ಲದು, ಇದೇ ಇದರ ಅರ್ಥ. ಕೋಷ್ಟಕ ಕ್ರ. 2 ರಲ್ಲಿ ತೋರಿಸಿದಂತೆ ಅದರ ಗ್ರಾಫ್ ತಯಾರಾಗಬಲ್ಲದು. ಇದನ್ನು ರೇಕ್ ಎಂಗಲ್ ನ ಮುಖ್ಯ ಪರಿಣಾಮದ ಗ್ರಾಫ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

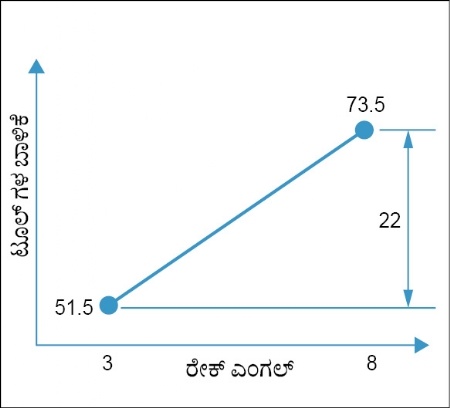
ಗ್ರಾಫ್ ಕ್ರ. 1

ಇದರಂತೆಯೇ ಎರಡನೇ ಘಟಕಗಳ ಪ್ರಭಾವವನ್ನು ಈ ಮುಂದೆ ನೀಡಿರುವ ಅಳತೆ ಮಾಡಬಹುದು.

• 60 ಕಟಿಂಗ್ ಸ್ಪೀಡ್ ನಲ್ಲಿ ಟೂಲ್ ಸರಾಸರಿ ಆಯುಷ್ಯ (43+52)/2 = 47.5

• 40 ಕಟಿಂಗ್ ಸ್ಪೀಡ್ ನಲ್ಲಿ ಟೂಲ್ ಸರಾಸರಿ ಆಯುಷ್ಯ (60+95)/2 = 77.5

• ಇದೇ ರೀತಿಯಲ್ಲಿ ಕಟಿಂಗ್ ಸ್ಪೀಡ್ ನ ಪರಿಣಾಮ (47.5-77.5) = - 30

ಕಟಿಂಗ್ ಸ್ಪೀಡ್ 40 ರಿಂದ 60 ರ ತನಕ ಹೆಚ್ಚಾದಲ್ಲಿ ಟೂಲ್ ನ ಬಾಳಿಕೆಯು ಕಡಿಮೆಯಾಗುತ್ತದೆ, ಇದೇ ಮೈನಸ್ ಚಿಹ್ನೆಯ ಅರ್ಥ. ಇದನ್ನು ಗ್ರಾಫ್ ಕ್ರ. 2 ರಲ್ಲಿ ತೋರಿಸಲಾಗಿದೆ. ಕಟಿಂಗ್ ಸ್ಪೀಡ್ ಇದು ಪ್ರಮುಖವಾದ ಪರಿಣಾಮದ ಗ್ರಾಫ್ ಆಗಿರುತ್ತದೆ.

ಇದೇ ರೀತಿಯಲ್ಲಿ ಡಿಸೈನ್ ಮಾಡಿರುವ ಪ್ರಯೋಗಗಳಲ್ಲಿ ನಾವು ಎಲ್ಲ ಘಟಕಗಳ ಸೆಟಿಂಗ್ ಒಂದೇ ಬಾರಿ ಬದಲಾಯಿಸಬಲ್ಲೆವು ಮತ್ತು ಆದರೂ ಕೂಡಾ ಪ್ರತಿಯೊಂದು ಘಟಕಗಳ ಪ್ರಭಾವವು ಸ್ವತಂತ್ರವಾಗಿ ಸಿಗಬಲ್ಲದು.

ಈಗ ನಾವು ಇಂಟರೇಕ್ಷನ್ ಕುರಿತು ತಿಳಿದುಕೊಳ್ಳೋಣ. ಇಂಟರೇಕ್ಷನ್ ಅಂದರೆ ಒಂದೇ ಘಟಕಗಳ ಪ್ರಭಾವವು ಇನ್ನೊಂದು ಘಟಕಗಳ ಸೆಟಿಂಗ್ ನಲ್ಲಿ ಅವಲಂಬಿಸಿರುವುದು. ಉದಾಹರಣೆ, ಕಟಿಂಗ್ ಸ್ಪೀಡ್ ನ ಪ್ರಭಾವವು ರೇಕ್ ಎಂಗಲ್ ನಲ್ಲಿ ಅವಲಂಬಿಸಿರಬಲ್ಲದು, ಕಾರಣ ಟೂಲ್ ನ ಎಡ್ಜ್ ಗಳಲ್ಲಿ ಬಿಲ್ಟ್ ಅಪ್ ಆಗುವುದು, ಇದೂ ರೇಕ್ ಎಂಗಲ್ ನಲ್ಲಿ ಅವಲಂಬಿಸಿರುತ್ತದೆ. ಅಥವಾ ಕಟಿಂಗ್ ಫೋರ್ಸ್ ನಲ್ಲಿ ಉಂಟಾಗುವ ಇಳಿತ. ತಾವು ಮಾಡಿರುವ ಪ್ರಯೋಗಕ್ಕೆ ಆಧರಿಸಿರುವ ಇಂಟರೇಕ್ಷನ್ ಕುರಿತು ತಿಳಿಯಲು ಘಟಕಗಳ ಸ್ತರಗಳಿಗೆ ಕೆಲವು ಕೋಡ್ ಗಳನ್ನು ನಿರ್ದೇಶಿಸಬೇಕಾಗುತ್ತದೆ. ಮೈನಸ್ ಗೋಸ್ಕರ (-1) ಮತ್ತು ಪ್ಲಸ್ ಗೋಸ್ಕರ (+1) ಎಂಬ ಕೋಡ್ ಗಳನ್ನು ನಿರ್ಧರಿಸಬೇಕು. ಘಟಕಗಳ ಅಂಕಣದಲ್ಲಿ ಅಂಕೆಗಳನ್ನು ಪರಸ್ಪರ ಗುಣಿಸಿದಾಗ ಇಂಟರೇಕ್ಷನ್ ಅಂಕಣದಲ್ಲಿ ಧನಾತ್ಮಕ/

ಋಣಾತ್ಮಕ (ಪಾಸಿಟಿವ್/ ನಿಗೆಟಿವ್) ಚಿಹ್ನೆಗಳೊಂದಿಗೆ ಸ್ತರದ ಅಂಕೆಗಳು ಲಭಿಸುತ್ತವೆ. ಕೋಷ್ಟಕ ಕ್ರ. 4 ರಲ್ಲಿ ಈ ಇಂಟರೇಕ್ಷನ್ ಕುರಿತಾದ ಹೆಚ್ಚುವರಿ AB ಅಂಕಣವನ್ನು ತೋರಿಸಲಾಗಿದೆ.

ಇಂಟರೇಕ್ಷನ್ ನ ಗಣನೆಯು ಈ ಹಿಂದಿನಂತಿದೆ ಮತ್ತು ಅದರಲ್ಲಿಯೂ ಪ್ಲಸ್ (+1) ಮತ್ತು ಮೈನಸ್ (-1) ಸ್ತರದಲ್ಲಿ ವ್ಯತ್ಯಾಸವಿರುವ ಮುಂಚಿನ ಸೂತ್ರವನ್ನೇ ಬಳಸಲಾಗುತ್ತದೆ. ಇದರಿಂದಾಗಿ ಇಂಟರೇಕ್ಷನ್ ಈ ಮುಂದಿನಂತಿರಬಲ್ಲದು.

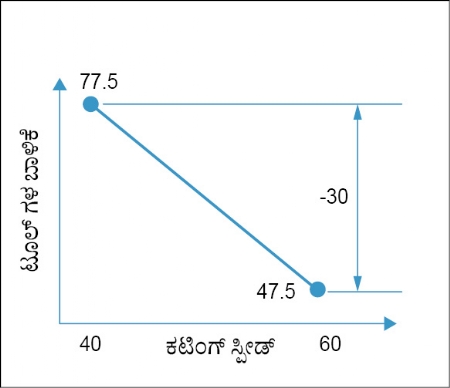
ಗ್ರಾಫ್ ಕ್ರ. 2

ಈ ಗಣನೆಗಳಿಗೆ ಅನುಸಾರವಾಗಿ ಕಟಿಂಗ್ ಸ್ಪೀಡ್ ಮತ್ತು ರೇಕ್ ಎಂಗಲ್ ಇವುಗಳಲ್ಲಿರುವ ಇಂಟರೇಕ್ಷನ್ ತುಂಬಾ ಹೆಚ್ಚಿರುತ್ತದೆ, ಎಂಬುದಾಗಿ ಕಂಡುಬರುತ್ತದೆ. ಈ ಘಟಕಗಳ ಮುಖ್ಯ ಪ್ರಭಾವಕ್ಕಿಂತಲೂ ಇದು ಹೆಚ್ಚಾಗಿದೆ.

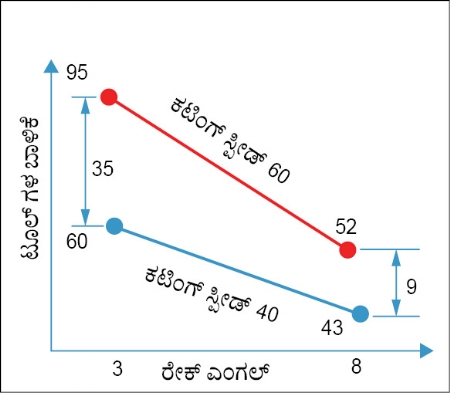
ಗ್ರಾಫ್ ಕ್ರ. 3

ಈ ಪ್ರಯೋಗದಲ್ಲಿ ರೇಕ್ ಎಂಗಲ್ ಮತ್ತು ಕಟಿಂಗ್ ಸ್ಪೀಡ್ ಇವುಗಳಲ್ಲಿರುವ ಇಂಟರೇಕ್ಷನ್ ಗ್ರಾಫ್ ಕ್ರ. 3 ರಲ್ಲಿ ತೋರಿಸಲಾಗಿದೆ. ಸಮಾನಾಂತರ ರೇಖೆಗಳ ಅರ್ಥವೆಂದರೆ, ಯಾವುದೇ ಇಂಟರೇಕ್ಷನ್ ಇಲ್ಲ ಎಂದಾಗುತ್ತದೆ. ಹಾಗೆಯೇ ಈ ರೇಖೆಗಳಲ್ಲಿರುವ ಕೋನ ಆ ಘಟಕಗಳಲ್ಲಿರುವ ಇಂಟರೇಕ್ಷನ್ ಎಷ್ಟು ಪ್ರಭಾವಶಾಲಿಯಾಗಿದೆ, ಎಂಬುದನ್ನು ಸೂಚಿಸುತ್ತದೆ. ಕಟಿಂಗ್ ಸ್ಪೀಡ್ ಮತ್ತು ರೇಕ್ ಎಂಗಲ್ ಇವುಗಳಲ್ಲಿರುವ ಇಂಟರೇಕ್ಷನ್ ಉಚ್ಚಮಟ್ಟದಲ್ಲಿ ಪ್ರಭಾವಶಾಲಿಯಾಗಿದೆ, ಎಂಬ ಅಂಶವು ಸ್ಪಷ್ಟವಾಗುತ್ತದೆ.

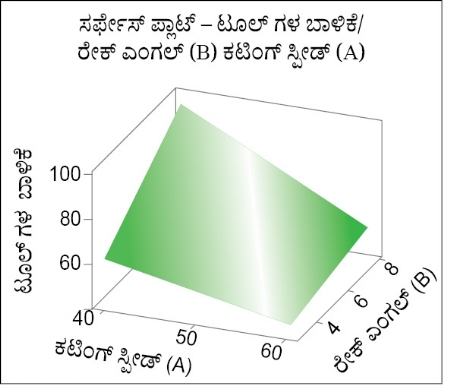
ಗ್ರಾಫ್ ಕ್ರ. 4

ಇಂಟರೇಕ್ಷನ್ ಪ್ಲಾಟ್ ನ ಗ್ರಾಫ್ ನಲ್ಲಿ ಪ್ರಸ್ತುತಿಯು ಮುಖ್ಯ ಪ್ರಭಾವಕ್ಕಿಂತ ಬೇರೆ ರೀತಿಯಲ್ಲಿ ಮಾಡಲಾಗುತ್ತದೆ. ಒಂದೇ ಘಟಕದ ಪ್ರಭಾವವನ್ನು ಇನ್ನೊಂದು ಘಟಕದ ಪ್ರತಿಯೊಂದು ಸೆಟಿಂಗ್ ನಲ್ಲಿ ಸ್ವತಂತ್ರವಾಗಿ ಅಳತೆ ಮಾಡಲಾಗುತ್ತದೆ. ಉದಾಹರಣೆ, ರೇಕ್ ಎಂಗಲ್ 3° ಯಲ್ಲಿ ಬದಲಾಯಿಸಿ 8° ಯಲ್ಲಿ ಸೆಟ್ ಮಾಡಿದ ನಂತರ

ಉಂಟಾಗುವ ಕಟಿಂಗ್ ಸ್ಪೀಡ್ ನ ಪ್ರಭಾವವನ್ನು ಅಳತೆ ಮಾಡಲಾಗುತ್ತದೆ. ಈ ಎರಡೂ ಪ್ರಭಾವಗಳಲ್ಲಿರುವ ವ್ಯತ್ಯಾಸದ ಅರ್ಧ ಮೌಲ್ಯವು ಇಂಟರೇಕ್ಷನ್ ನಲ್ಲಿ ಪ್ರಭಾವವನ್ನು ಬೀರುತ್ತದೆ. ರೇಕ್ ಎಂಗಲ್ 3° ಇರುವಾಗ ಕಟಿಂಗ್ ಸ್ಪೀಡ್ 40 ರಿಂದ 60 ಮಾಡಿದ್ದರಿಂದ ಲಭಿಸುವ ಪ್ರಭಾವ 35 ಇದೆ. ಇದನ್ನು ಗ್ರಾಫ್ ಕ್ರ. 3 ರಲ್ಲಿ ತೋರಿಸಲಾಗಿದೆ. ಅಲ್ಲದೇ ರೇಕ್ ಎಂಗಲ್ 8 ಇರುವಾಗ ಕಟಿಂಗ್ ಸ್ಪೀಡ್ 40 ರಿಂದ 60 ಮಾಡಿದ್ದರಿಂದ ಲಭಿಸುವ ಪ್ರಭಾವ 9 ಆಗಿದೆ. ರೇಕ್ ಎಂಗಲ್ 8° ಇರುವಾಗ ಕಟಿಂಗ್ ಸ್ಪೀಡ್ ನ ಪ್ರಭಾವವು ರೇಕ್ ಎಂಗಲ್ 3° ರಲ್ಲಿರುವ ಪ್ರಭಾವಕ್ಕಿಂತ ತುಂಬಾ ಕಡಿಮೆ ಇದೆ, ಎಂಬುದೇ ಇದರ ಅರ್ಥ. ಈ ಎರಡೂ ಪ್ರಭಾವಗಳಲ್ಲಿರುವ ವ್ಯತ್ಯಾಸದ ಭಾಗವು (9-35)/ 2 = -26/ 2 = -13 ಆಗಿರುತ್ತದೆ. ಈ ರೀತಿಯಲ್ಲಿ ಇಂಟರೇಕ್ಷನ್ ನ ಪ್ರಭಾವ –13 ಇರುತ್ತದೆ.

ಟೂಲ್ ನ ಬಾಳಿಕೆಯನ್ನು ವೃದ್ಧಿಸುವುದೇ ನಮ್ಮ ಅಂತಿಮ ಉದ್ದೇಶವಾಗಿದೆ. ಇದಕ್ಕೋಸ್ಕರ ನಾವು ಮಿನಿಟ್ಯಾಬ್ ನಂತಹ ಸಾಫ್ಟ್ ವೇರ್ ಬಳಸಿ ಕ್ಲಿಷ್ಟವಾಗಿರುವ ಸಂಖ್ಯಾಶಾಸ್ತ್ರೀಯ ಗಣನೆಯನ್ನು ಮಾಡಬಲ್ಲೆವು. ಗ್ರಾಫ್ ಕ್ರ. 4 ರಲ್ಲಿ ಘಟಕಗಳ ಸರ್ಫೇಸ್ ಪ್ಲಾಟ್ ತೋರಿಸಲಾಗಿದೆ. ಈ ಪ್ಲಾಟ್ ನಲ್ಲಿರುವ ವಕ್ರಭಾಗವು ಉಲ್ಲೇಖಿಸುವಂತಿದೆ. ಈ ಎರಡೂ ಘಟಕಗಳಲ್ಲಿರುವ ಪ್ರಭಾವಶಾಲಿಯಾದ ಇಂಟರೇಕ್ಷನ್ ನಿಂದಾಗಿ ಹಾಗಾಗಿದೆ.

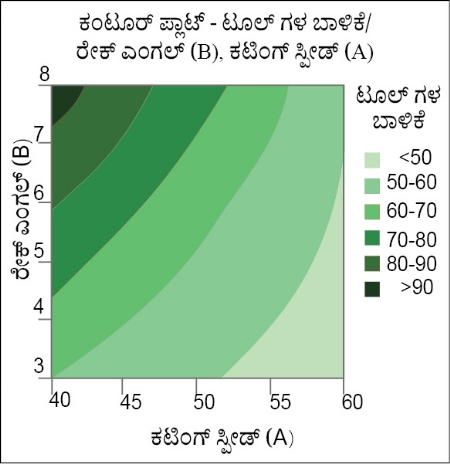
ಗ್ರಾಫ್ ಕ್ರ. 5

ಗ್ರಾಫ್ ಕ್ರ. 5 ರಲ್ಲಿ ತೋರಿಸಿರುವ ಕಂಟೂರ್ ಪ್ಲಾಟ್ ಈ ಘಟಕಗಳ ಪರಸ್ಪರ ಫಲಿತಾಂಶವನ್ನು ನೋಡುವ ಸುಲಭವಾದ ದಾರಿಯಾಗಿದೆ. ಇದರಲ್ಲಿ ಎಲ್ಲಕ್ಕಿಂತಲೂ ದೃಢವಾದ ಝೋನ್ ನಲ್ಲಿ ಟೂಲ್ ಗೆ ಗರಿಷ್ಠ ಪ್ರಮಾಣದ ಬಾಳಿಕೆಯು ಲಭಿಸಬಲ್ಲದು, ಎಂಬುದನ್ನು ಅಪೇಕ್ಷಿಸಲಾಗಿದೆ. ಸಾಫ್ಟ್ ವೇರ್ ನಲ್ಲಿ ಆಪ್ಟಿಮೈಜರ್ ಬಳಸಿ ಟೂಲ್ ಗಳಿಗೆ ಗರಿಷ್ಠ ಪ್ರಮಾಣದಲ್ಲಿ ಬಾಳಿಕೆಯನ್ನು ನೀಡಬಲ್ಲ ಸೆಟಿಂಗ್ ಹುಡುಕುವುದೇ, ಅಂತಿಮ ಗುರಿಯಾಗಿದೆ. 40 ಇದು ಕಟಿಂಗ್ ಸ್ಪೀಡ್ ಮತ್ತು 8° ಇದು ರೇಕ್ ಎಂಗಲ್ ಈ ರೀತಿಯ ಸೆಟಿಂಗ್ ನಲ್ಲಿ ಟೂಲ್ ಗೆ ಗರಿಷ್ಠ ಬಾಳಿಕೆಯು ಸಿಗುತ್ತದೆ, ಎಂಬುದು ಇಲ್ಲಿ ಸ್ಪಷ್ಟವಾಗಿ ಗಮನಕ್ಕೆ ಬರುತ್ತದೆ. ಘಟಕಗಳ ಸಂಖ್ಯೆಯು ಹೆಚ್ಚು ಇರುವಾಗ ಮತ್ತು ತುಂಬಾ ಹೆಚ್ಚು ಇಂಟರೇಕ್ಷನ್ ಇರುವಾಗ ಆಪ್ಟಿಮೈಜ್ಡ್ ಸೆಟಿಂಗ್ ಹುಡುಕುವುದು ಅಸಾಧ್ಯವಾಗಿರುತ್ತದೆ. ಇದೇ ಸಮಯದಲ್ಲಿ ಸಾಫ್ಟ್ ವೇರ್ ತಕ್ಷಣ ಉತ್ತರವನ್ನು ನೀಡುತ್ತದೆ. ಅನೇಕ ಬಾರಿ ಒಂದಕ್ಕಿಂತ ಹೆಚ್ಚು ಫಲಿತಾಂಶಗಳ ಆಪ್ಟಿಮೈಜೆಶನ್ ಮಾಡಬೇಕಾಗಿರುತ್ತದೆ ಮತ್ತು ಅದನ್ನು ಗಮನದಲ್ಲಿಟ್ಟುಕೊಂಡು ಮಾಡುವುದೂ ಸುಲಭವಾಗಿರುವುದಿಲ್ಲ. ಈ ಪರಿಸ್ಥಿತಿಯಲ್ಲಿ ಸಾಫ್ಟ್ ವೇರ್ ನ ಸಹಾಯವನ್ನು ಪಡೆಯುವುದು ತುಂಬಾ ಉಪಯುಕ್ತವಾಗಿರುತ್ತದೆ.

ಸಂಖ್ಯಾ ಶಾಸ್ತ್ರಜ್ಞರಿಂದ ಘಟಕಗಳು ಮತ್ತು ಸ್ತರ ಇವುಗಳ ಸಂಖ್ಯೆಗಳಿಗೆ ಅನುಸಾರವಾಗಿ ಪ್ರಯೋಗಗಳಿಗೋಸ್ಕರ ವಿಶಿಷ್ಟ ರೀತಿಯ ಡಿಸೈನ್ ತಯಾರಿಸಲಾಗಿವೆ. ಸಾಮಾನ್ಯವಾಗಿ ಪ್ರಯೋಗಗಳ ಡಿಸೈನ್ ಮತ್ತು ವಿಶ್ಲೇಷಣೆಯನ್ನು ಮಾಡಲು ವ್ಯಾವಸಾಯಿಕ ಸ್ತರದಲ್ಲಿ ಮಿನಿಟ್ಯಾಬ್ ನಂತಹ ಸಾಫ್ಟ್ ವೇರ್ ಬಳಸಲಾಗುತ್ತದೆ. ಇವುಗಳಿಂದ ಎಲ್ಲಕ್ಕಿಂತಲೂ ಇಷ್ಟಪಟ್ಟಿರುವ ಮತ್ತು ಸ್ಥಿರವಾದ ಪರಿಣಾಮಗಳು ಲಭಿಸಬಲ್ಲವು, ಇಂತಹ ಘಟಕಗಳ ಸೆಟಿಂಗ್ ನ ಅಂದಾಜನ್ನು ತಿಳಿದುಕೊಳ್ಳಲು ಅನೇಕ ಹೆಚ್ಚುವರಿ ವೈಶಿಷ್ಟ್ಯಗಳು ಸಾಫ್ಟ್ ವೇರ್ ನಲ್ಲಿ ಲಭ್ಯವಿವೆ.

ಘಟಕಗಳ ಸಂಖ್ಯೆ ಹೆಚ್ಚಿದ್ದರೂ ಕೂಡಾ, ಹೆಚ್ಚಿನ ಸಂಖ್ಯೆಯಲ್ಲಿ ಪರೀಕ್ಷೆಗಳನ್ನು ಮಾಡಬೇಕಾಗುತ್ತದೆ, ಎಂದು ಅನಿಸುವುದು ಸಹಜ. ಆದರೂ ಕೂಡಾ ಬೃಹತ್ ಸಂಖ್ಯೆಯ ಘಟಕಗಳಿರುವ ಪ್ರಶ್ನೆಗಳಿಗೆ ಉತ್ತರವನ್ನು ಅಥವಾ ಪರಿಹಾರವನ್ನು ಹುಡುಕಲು ಸಂಖ್ಯಾ ಶಾಸ್ತ್ರಜ್ಞರು ಫ್ರೇಕ್ಷನಲ್ ಫ್ಯಾಕ್ಟೋರಿಯಲ್ ಡಿಸೈನ್ ಅಭಿವೃದ್ಧಿ ಮಾಡಿದ್ದಾರೆ. ಸಾಫ್ಟ್ ವೇರ್ ನ ಮೂಲಕ ಅದನ್ನು ಸಹಜವಾಗಿ ಬಳಸಬಹುದು.

9822014488

hemant@world-class-quality.com

ಹೇಮಂತ್ ಊರ್ಧ್ವರೇಷೆ ಇವರು ಕಮಿನ್ಸ್ ಇಂಡಿಯಾ ಲಿಮಿಟೆಡ್ ಎಂಬ ಕಂಪನಿಯಲ್ಲಿದ್ದರು. ಇವರು ಜನರಲ್ ಮ್ಯಾನೆಜರ್ ಕ್ವಾಲಿಟಿ ಹಾಗೆಯೇ ಹೆಡ್ ಆಫ್ ಇಂಜಿನಿಯರಿಂಗ್ ಹುದ್ದೆಗಳಲ್ಲಿ ಸೇವೆಯನ್ನು ಸಲ್ಲಿಸಿದ್ದಾರೆ.