ಇಂಜಿನಿಯರಿಂಗ್ ಡ್ರಾಯಿಂಗ್ ಕುರಿತಾದ ಅಂಶಗಳು - 2

 

 

 

ಅನೇಕ ಹೆಸರಾಂತ ಕಂಪನಿಗಳ ಉತ್ಪಾದನೆಗಳು ಸ್ಟ್ಯಾಂಡರ್ಡ್ ಕೆಟೆಲಾಗ್ ಗೆ ಅನುಸಾರವಾಗಿ ತಯಾರಿಸಲಾಗುತ್ತವೆ. ಅದರ ಅಳತೆ, ಮಾಪನಗಳನ್ನು ನಿಗದಿತ ರೀತಿಯಲ್ಲಿಯೇ ಮಾಡಲವಾಗುತ್ತದೆ. ಉದಾಹರಣೆ, ‘O’ ರಿಂಗ್ಸ್, ಗೇಸ್ಕೆಟ್, ಪಾಸ್ಟನರ್ ಮುಂತಾದವುಗಳನ್ನು ತಯಾರಿಸುವ ಕಂಪನಿಗಳ ಉತ್ಪಾದನೆಗಳು ಅಲ್ಪಸ್ವಲ್ಪ ವ್ಯತ್ಯಾಸದಲ್ಲಿ ಪುನರಾವರ್ತನೆ ಆಗುವಂತಹದ್ದಿರುತ್ತವೆ. ಒಮ್ಮೊಮ್ಮೆ ಉದ್ದ, ಆದರೆ ಇನ್ನೊಮ್ಮೆ ವ್ಯಾಸದಲ್ಲಿ ಬದಲಾವಣೆ. ಇನ್ನಿತರ ಎಲ್ಲ ಘಟಕಗಳು ಸಮಾನವಾಗಿರುತ್ತವೆ. ಒಮ್ಮೊಮ್ಮೆ ಎಲ್ಲ ಮಾಪನಗಳು ಸಮಾನ ಆದರೆ ಕಚ್ಚಾ ವಸ್ತುಗಳನ್ನು ಮಾತ್ರ ಬೇರೆಯೇ ಸಾಮಗ್ರಿಗಳಿಂದ ತಯಾರಿಸುವುದಾಗಿರುತ್ತದೆ. ಇದಕ್ಕೋಸ್ಕರ ಪ್ರತಿಯೊಂದು ಬಾರಿ ಹೊಸ ಡ್ರಾಯಿಂಗ್ ತಯಾರಿಸುವ ಆವಶ್ಯಕತೆ ಇರುತ್ತದೆ. ಇದರ ಹೊರತಾಗಿ ಇದಕ್ಕೋಸ್ಕರ ಬೇಕಾಗುವ ಸಮಯವೂ ಪೂರೈಸುವುದಿಲ್ಲ. ಇದಕ್ಕೋಸ್ಕರವೇ ದಿನನಿತ್ಯದ ಡ್ರಾಯಿಂಗ್ ಗೋಸ್ಕರ ಪ್ಯಾರಾಮೆಟ್ರಿಕ್ ಡ್ರಾಯಿಂಗ್ ಎಂಬ ಕಲ್ಪನೆಯು ಪ್ರಚಲಿತವಾಗುತ್ತಿದೆ. ಪ್ಯಾರಾಮೆಟ್ರಿಕ್ ಡ್ರಾಯಿಂಗ್ ನ ಸಹಾಯದಿಂದ ಹೊಸ ವಿನ್ಯಾಸವನ್ನು ಮಾಡಲು ಅಥವಾ ಈ ಹಿಂದೆ ಮಾಡಿಟ್ಟಿರುವ ಡ್ರಾಯಿಂಗ್ ನಲ್ಲಿ ಬದಲಾವಣೆಗಳನ್ನು ಮಾಡಲು ಇದನ್ನು ಬಳಸಿದಲ್ಲಿ ಖಂಡಿತವಾಗಿಯೂ ಲಾಭವಾಗಬಲ್ಲದು. ಮೊದಲಾಗಿ ಪ್ಯಾರಾಮೆಟ್ರಿಕ್ ಡ್ರಾಯಿಂಗ್ ಕುರಿತಾದ ಒಂದು ಉದಾಹರಣೆಯನ್ನು ನೋಡೋಣ.

 

‘ABCD’ ಎಂಬ ಹೆಸರಿನ ಆಯತಾಕಾರವನ್ನು ಇದಕ್ಕೋಸ್ಕರ ಚುನಾಯಿಸಲಾಯಿತು. ಆದರೆ ಡ್ರಾಯಿಂಗ್ ನಲ್ಲಿ ಆಯತಾಕಾರದ ವಿನ್ಯಾಸವನ್ನು ತಯಾರಿಸಲು ಅದರ ಉದ್ದ, ಅಗಲ ಮತ್ತು ದಪ್ಪ ಇವುಗಳನ್ನು ತಿಳಿದುಕೊಳ್ಳುವುದು ಅತ್ಯಾವಶ್ಯಕವಾಗಿದೆ. ಯೋಜನೆಯನ್ನು ತಯಾರಿಸುವಾಗ ಅದರ ಮಾಪನದ ಸಮೀಕರಣವನ್ನು ಬಳಸಿ, ಸರಿಹೊಂದಾಣಿಸಿ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ. ಪ್ಯಾರಾಮೆಟ್ರಿಕ್ ಡ್ರಾಯಿಂಗ್ ನಲ್ಲಿ ಅದರ ಉದ್ದದೊಂದಿಗೆ ಅಗಲಕ್ಕೆ ಇರುವ ಅನುಪಾತವನ್ನು ನಿರ್ಧರಿಸುವುದೂ ಅತ್ಯಂತ ಮಹತ್ವದ್ದಾಗಿದೆ. ಇದಕ್ಕೋಸ್ಕರ ಈ ಕೆಳಗಿನ ಉದಾಹರಣೆಯನ್ನು ತಿಳಿದುಕೊಳ್ಳೋಣ.

 

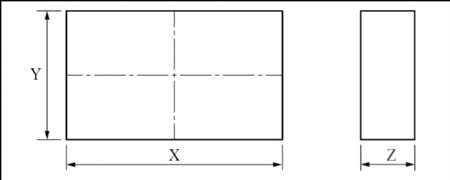
I. ಉದ್ದಕ್ಕೆ X, ಅಗಲಕ್ಕೆ Y ಮತ್ತು ದಪ್ಪಕ್ಕೆ Z ಎಂಬುದಾಗಿ ತಿಳಿಯಿರಿ.

II. ಉದ್ದ ಮತ್ತು ಅಗಲದ ಅನುಪಾತ ನಿರ್ಧರಿಸೋಣ

Y = (X x 0.6)

III. ಉದ್ದ ಮತ್ತು ದಪ್ಪದ ಅನುಪಾತವನ್ನು ನಿರ್ಧರಿಸೋಣ

Z = (X x 0.25)

 

 

ಇದನ್ನು ತಿಳಿದುಕೊಳ್ಳಲು ಚಿತ್ರ ಕ್ರ. 1 ವೀಕ್ಷಿಸಿರಿ.

 

ಚಿತ್ರ ಕ್ರ. 1

 

ಮೇಲಿನ ಮೂರು ಸಮೀಕರಣಗಳಿಗೆ ಅನುಸಾರವಾಗಿ ಆಯತದ ಉದ್ದ, ಅಗಲ ಮತ್ತು ದಪ್ಪವನ್ನು ನಿರ್ಧರಿಸಲಾಯಿತು. ಇದಕ್ಕೆ ಅನುಸಾರವಾಗಿ ಅವುಗಳಲ್ಲಿ ಪರಸ್ಪರ ಸಂಬಂಧ ನಿರ್ಮಾಣವಾಯಿತು. ಈಗ ಉದ್ದದಲ್ಲಿ ಬದಲಾವಣೆಯನ್ನು ಮಾಡುವುದಾದಲ್ಲಿ ಅದರ ಅಗಲ ಮತ್ತು ದಪ್ಪವು ನಿರ್ಧರಿಸಿದ ಅನುಪಾತಕ್ಕೆ ಅನುಸಾರವಾಗಿ ತನ್ನಷ್ಟಕ್ಕೆ ಬದಲಾಗುತ್ತದೆ. ಇದರಿಂದಾಗಿ ಲಭಿಸುವ ಉಪಯುಕ್ತತೆ ಈ ಮುಂದಿನಂತಿದೆ.

·        ಈ ರೀತಿಯ ಎಲ್ಲ ಬದಲಾವಣೆಗಳನ್ನು ಮಾಡುವಲ್ಲಿ ಕಟ್, ಕಾಪಿ, ಪೇಸ್ಟ್, ಡಿಲಿಟ್ ಇಂತಹ ಯಾವುದೇ ಕಮಾಂಡ್ ಗಳ ಬಳಕೆಯನ್ನು ನಿಯೋಜಿತವಾಗಿ ನಿಲ್ಲಿಸಬಹುದು.

·        ತುಂಬಾ ಕಡಿಮೆ ಸಮಯದಲ್ಲಿಯೇ ಇಂತಹ ಬದಲಾವಣೆಗಳನ್ನು ಮಾಡಬಹುದು.

·        ತಪ್ಪುಗಳ ಪ್ರಮಾಣವು ಕಡಿಮೆಯಾಗಬಲ್ಲದು.

·        ಡ್ರಾಯಿಂಗ್ ದೃಢೀಕರಿಸುವ ಅಭ್ಯಾಸವಾಗಬಲ್ಲದು.

ಆಯತಾಕಾರದಂತೆ ಉರುಟು, ಚೌಕೋನ, ತ್ರಿಕೋನ, ಷಟ್ಕೋನ ಇಂತಹ ವಿವಿಧ ಆಕಾರದ ಪ್ಯಾರಾಮೆಟ್ರಿಕ್ ಪದ್ಧತಿಯಿಂದಲೂ ನಿಯಂತ್ರಿಸಬಹುದು. ಆಯತದಂತಹ ವಿಶಿಷ್ಟ ರೀತಿಯ ಆಕಾರಕ್ಕೆ ಪ್ಯಾರಾಮೆಟ್ರಿಕ್ ಪದ್ಧತಿಯಲ್ಲಿ ವಿನ್ಯಾಸವನ್ನು ಮಾಡಲಾಯಿತು, ಹಾಗೆಯೇ ಸಂಪೂರ್ಣ ವಸ್ತುವನ್ನು ಪ್ಯಾರಾಮೆಟ್ರಿಕ್ ಪದ್ಧತಿಯಲ್ಲಿಯೂ ತಯಾರಿಸಬಲ್ಲೆವು. ಇದಕ್ಕೋಸ್ಕರ ಒಂದು ವಸ್ತುವಿನ ಉದಾಹರಣೆಯ ಅಭ್ಯಾಸವನ್ನು ಮಾಡಬಹುದು.

 

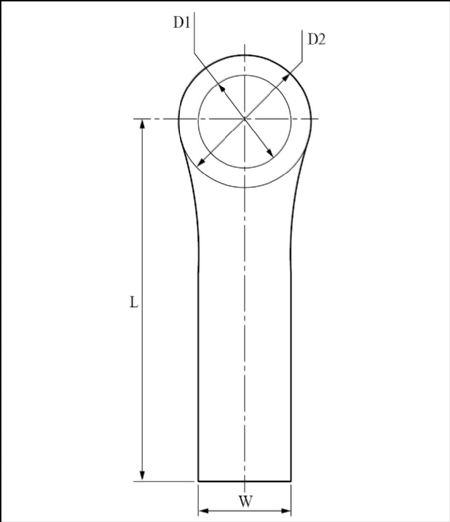
ಚಿತ್ರ ಕ್ರ. 2

 

ಚಿತ್ರ ಕ್ರ. 2 ರಲ್ಲಿ ಬೇರೆಬೇರೆ ಆಕಾರಗಳು ಸೇರ್ಪಡಿಸಲ್ಪಟ್ಟಿವೆ. ಇದೇ ಆಕಾರವನ್ನು ಪರಸ್ಪರ ಅಳತೆಗಳಲ್ಲಿ ಅವಲಂಬಿಸುವಾಗ ಅದರಿಂದ ಲಭಿಸುವ ಆಯಾಮಗಳನ್ನು ನಿರ್ಧರಿಸಿದಾಗ ಒಂದು ಆಕಾರದಲ್ಲಿ ಬದಲಾವಣೆ ಮಾಡಿದಾಗ ಇನ್ನೊಂದು ಆಕಾರ ಅದರ ನಿಗದಿತ ಅನುಪಾತ ಬದಲಾಯಿಸಬಲ್ಲದು. ಇದರಲ್ಲಿರುವ ಉದ್ದ ‘L’ ಯಿಂದ ಮತ್ತು ಅಗಲ ‘W’ ಇದನ್ನು ತೋರಿಸಲಾಗಿದೆ. ಉದ್ದದೊಂದಿಗೆ ಇರುವ ಅಗಲದ ಅನುಪಾತ ನಿರ್ಧರಿಸುವುದು ಅತ್ಯಾವಶ್ಯಕವಾಗಿದೆ. ಅದನ್ನು ನಾವು ತಮ್ಮ ಯೋಜನೆಗೆ ಅನುಸಾರವಾಗಿ ಮತ್ತು ಅಂಕೆ-ಸಂಖ್ಯೆಗಳಲ್ಲಿ ನಿರ್ಧಿರಿಸಬಲ್ಲೆವು. ಇದಕ್ಕೋಸ್ಕರ ನಿರ್ಧಾರಿತ ಸೂತ್ರವಿರುವುದು ಅತ್ಯಾವಶ್ಯಕವಾಗಿದೆ.

ಅದು ಹೇಗೆಂದರೆ,

 

W = L/4……….. ವಿಧಾನ i

ಒಂದು ವೇಳೆ, L = ಉದ್ದ = 40 ಮಿ.ಮೀ.

ವಿಧಾನ i ಗೆ ಅನುಸಾರವಾಗಿ,

W = 40/4

 

 

D2 = 1.25 x D1………….. ವಿಧಾನ i

ಎಲ್ಲಕ್ಕಿಂತಲೂ ಮೊದಲು ‘D1’ ಇದು ಮೂಲ ವ್ಯಾಸವಾಗಿದೆ. ಕಾರಣ ಈ ವಸ್ತುಗಳಲ್ಲಿರುವ ಒಳ ವ್ಯಾಸವು ಯಾವುದಾದರೂ ಇನ್ನೊಂದು ವಸ್ತುವಿನ ವ್ಯಾಸದೊಂದಿಗೆ ಜೋಡಿಸಲ್ಪಡಲಿದೆ. ಅದಕ್ಕೋಸ್ಕರವೇ ಈ ವ್ಯಾಸವು ಖಂಡಿತವಾಗಿಯೂ ಮಹತ್ವದ್ದಾಗಿದೆ. ಇದರಿಂದಾಗಿ ‘D1’ ಗೆ ಪ್ರಾಧಾನ್ಯತೆಯನ್ನು ನೀಡಿ ಅದನ್ನು ನಿರ್ಧರಿಸೋಣ.

ಒಂದು ವೇಳ, D1 = 15 ಮಿ.ಮಿ.

ವಿಧಾನ i ಅನುಸಾರವಾಗಿ

D2 = 1.25 x 15

= 18.75 ಮಿ.ಮೀ.

 

 

ಈಗ ಯಾವುದೊಂದು ಕಾರಣದಿಂದಾಗಿ ಭವಿಷ್ಯತ್ಕಾದಲ್ಲಿ ಇದರಲ್ಲಿ ಯಾವುದೇ ಘಟಕ, ಉದ್ದ, ವರ್ತುಲದ ಅಳತೆ ಇವುಗಳಲ್ಲಿ ಬದಲಾವಣೆಯಾದಲ್ಲಿ ಅದರೊಂದಿಗೆ ಸಂಬಂಧಪಟ್ಟ ಅನುಪಾತಕ್ಕೆ ಅನುಸಾರವಾಗಿ ಪರಿವರ್ತನೆಯಾಗಬಲ್ಲದು. ಇದರಿಂದಾಗಿ ತಮಗೆ ಮತ್ತೆ ಅಂಕೆ-ಸಂಖ್ಯೆಗಳನ್ನು ಪರಿಶೀಲಿಸುವ ಆವಶ್ಯಕತೆ ಇರುವುದಿಲ್ಲ. ಹಾಗೆಯೇ ಸಮಯದಲ್ಲಿಯೂ ಉಳಿತಾಯವಾಗಬಲ್ಲದು.

 

ಈ ಸಂಪೂರ್ಣ ಲೇಖನವು ಪ್ಯಾರಾಮೆಟ್ರಿಕ್ ಡ್ರಾಯಿಂಗ್ ಈ ಅತ್ಯಾಧುನಿಕ ಹಂತದಲ್ಲಿ ಅವಲಂಬಿಸಿರುತ್ತದೆ. ಈ ಪದ್ಧತಿಯಲ್ಲಿ ನಾವು ಸುಲಭವಾದ ಡ್ರಾಯಿಂಗ್ ನ ವಿನ್ಯಾಸವನ್ನು ಮಾಡಬಲ್ಲೆವು. ಕ್ಲಿಷ್ಟವಾದ ವಿನ್ಯಾಸಕ್ಕೆ ಈ ಪದ್ಧತಿಯು ಅಷ್ಟು ಸುಲಭವಿಲ್ಲ, ಕಾರಣ ಅನುಪಾತದಲ್ಲಿ ಬದಲಾವಣೆಯನ್ನು ಮಾಡಿದಲ್ಲಿ ಅದರಿಂದ ಉಂಟಾಗುವ ಪರಿಣಾಮದ ವ್ಯಾಪ್ತಿಯನ್ನು ಸೀಮಿತಗೊಳಿಸುವುದು ಅತ್ಯಂತ ಕಠಿಣವಾಗಬಲ್ಲದು. ಆದರೂ ಕೂಡಾ ಪ್ರತಿದಿನವೂ ಸುಲಭವಾದ ವಿನ್ಯಾಸವನ್ನು ಮಾಡುವಾಗ ಇದರ ಕುರಿತಾಗಿ ತಮಗೆ ಖಂಡಿತವಾಗಿಯೂ ಲಾಭವಾಗಬಲ್ಲದು.

 

ಮುಂದಿನ ಲೇಖನದಲ್ಲಿ ನಾವು ‘ಸ್ಟ್ಯಾಂಡರ್ಡ್ ಟೆಂಪ್ಲೇಟ್” ಹೇಗೆ ತಯಾರಿಸಬೇಕು, ಹಾಗೆಯೇ ಅದನ್ನು ತಯಾರಿಸುವಾಗ ಯಾವ ಘಟಕಗಳ ಕುರಿತು ಪ್ರಾಧಾನ್ಯತೆಯಿಂದ ವಿಚಾರ ಮಾಡುವುದು ಆವಶ್ಯಕವಾಗಿದೆಯೋ, ಇದರ ಕುರಿತಾದ ವಿಸ್ತಾರವಾದ ಮಾಹಿತಿಯನ್ನು ಅರಿತುಕೊಳ್ಳೋಣ.

 

9823389389